تصحيح الامتحان الوطني الموحد 2009

تمرين األول 3نقط الفضاء منسوب لمعلم متعامد ممنظم O i j k M النقط مجوعة Sو D0 1 -1 و C2 -1 0 و B6 6 0 و A-2 2 8 النقط نعتبر MAMB 0 التي تحقق و استنتج أن معادلة ديكارتية للمستوى OCD هي x2y2z0 OC OD 1 حدد احداثيات المتجهة OD01 1 و OC2 10 لدينا 1 1 2 1 2 0 0 1 0 1 1 1 122 OC OD OC OD معادلة ديكارتية للمستوى OCD 2 2 0 M x y z OCD OM OC OD x y z و شعاعها R 6 244 2 بين أن S فلكة مركزها AB و شعاعها منتصف القطعة S فلكة مركزها 2 AB R المركز 2 2 A B x x x 4 و 2 A B y y y 4 و 2 A B z z z 2 2 2 12 الشعاع AB x x y y z z B A B A B A اذن 6 2 AB R عن المستوى OCD 3 ا احسب مسافة النقطة 2 2 6 12 22 22 x y z d OCD ب استنتج أن المستوى OCD مماس للفلكة S S للفلكة مماس OCD المستوى فان d OCD R 6 بما أن OA OB 0 و استنتج أن النقطة هي نقطة O تماس الفلكة S والمستوى OCD ج تحقق أن OB660 و OA 2 28 لدينا OA OB 2 6 2 6 8 0 0 S للفلكة تنتمي O النقطة اذن OA OB 0 لدينا و لدينا النقطة O تنتمي للمستوى OCD اذن O هي نقطة تماس الفلكة S والمستوى OCD تصحيح االمتحان الوطني للباكالوريا األستاذ بوجغواد ثانوية الحسن الثاني بني مالل httpmathboujcla 2009 العادية الدورة

تمرين الثاني O u v المستوى منسوب لمعلم متعامد ممنظم مباشر و A a i 2 2 لتكن النقط 3 1 2 2 C c i 1 3 1 3 و B b i 1 أكتب على الشكل المثلثي العددين العقديين a و b 2 2 4 a و 5 1 6 b z bz 2ا بين أن 5 6 5 6 0 0 i i R M M z z e z ze z zb 5 6 5 1 6 i e b R A C ب بين ان 3 1 2 2 2 2 c1 3 1 3 R A C c ab c i i i arg arg arg 2 c a b 2 بين ان cab لدينا 3 ادن arg arg 2 arg arg arg 2 c ab c a b

httpmathboujcla تمرين ثالث يحتوي صندوق على 3 كرات بيضاء و 5 كرات حمراء و 4 كرات سودائء نسحب عشوائيا ثالث كرات بالتتابع و بدون من الصندوق 1 الحدث A الحصول على ثالث كرات من نفس اللون و الحدث B الحصول على ثالث كرات من كل لون بين أن 3 44 و p A 3 11 p B RRR أو NNN أو BBB A الحدث 333 3 4 5 3 12 3 44 CCC C PA BNR B الحدث PB 1 1 1 3 4 5 3 12 3 11 C C C C 2 ليكن المتغير العشوائي X اللذي يربط كل سحبة لثالث كرات بعدد األلوان التي تحملها أ حدد القيم التي يأخذها المتغير العشوائي X RRR أو NNN أو BBB A الحدث X1 RRR NNN أو BBB أو C الحدث X2 BNR B الحدث X3 ب حدد قانون احتمال المتغير العشوائي X و احسب االمل الرياضي EX 3 1 44 p X p A 2 1 2 1 2 1 3 9 4 8 5 7 3 12 29 2 44 C C C C C C p X p C C 12 3 44 p X p B 97 1 1 2 2 3 3 44 E X p X p X p X httpmathboujcla httpmathboujcla

تمرين رابع نضع 1 2 3 x I dx x و 1 2 J x dx ln2 6 1 أ تحقق أن 3 3 1 3 3 x x x x I 1 3ln 2 ان بين ب 1 1 1 2 2 2 ln 3 1 3ln 2 3 x I dx x x x 2 باستعمال المكاملة باألجزاء بين ان J -I 1 1 1 2 2 2 2 ln2 6 ln2 6 2 6 ln 4 2ln 2 x J x x dx x x dx x J I J I httpmathboujcla المسألة 2ln 2 2 بمايلي المعرفة f الدالة لتكن -I x x O i j و Cf منحناها في م م م f x e e 2 2 12 1 1 تحقق أن x x x Df ان واستنتج e e e 12 1 2 2 1 1 2 2 x x x x x e e e e e 2 2 0 12 1 0 D x x f x f x D e e e لدينا 2 2 2 2 12 1 1 0 x x x x x x x e e e e e e e

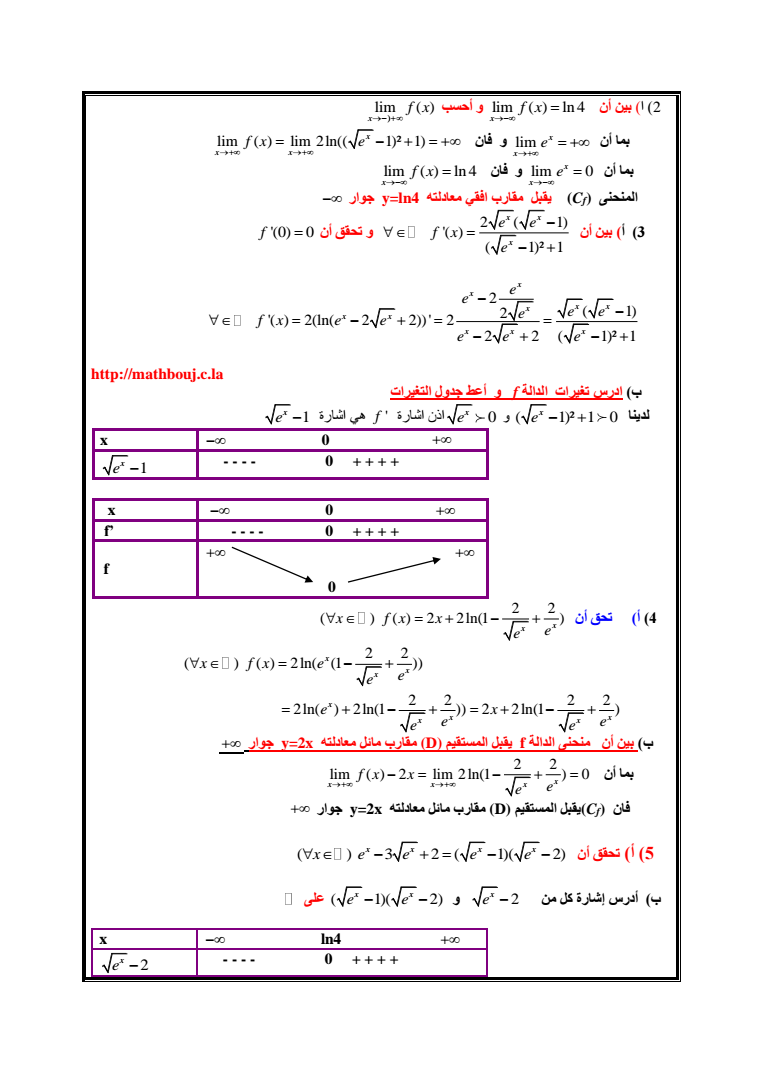
lim ln 4 2 ا بين أن x f x و أحسب lim x f x lim بما أن x x e lim lim 2ln 12 1 و فان x x x f x e lim 0 بما أن x x e lim ln 4 و فان x f x المنحنى Cf يقبل مقارب افقي معادلته yln4 جوار 3 أ بين أن 2 1 12 1 x x x e e f x e f 0 0 و تحقق أن 2 2 1 2ln 2 2 2 2 2 12 1 x x x x x x x x x x e e e e e f x e e e e e httpmathboujcla ب ادرس تغيرات الدالة f و أعط جدول التغيرات 12 1 0 لدينا x و e x 1 هي اشارة f اذن اشارة e x e x 1 x e - - - - 0 x f - - - - 0 f 4 أ تحق أن 2 2 2 2ln1 x x x f x x e e 2 2 2ln 1 2 2 2 2 2ln 2ln1 2 2ln1 x x x x x x x x x f x e e e e x e e e e ب بين أن منحنى الدالة f يقبل المستقيم D مقارب مائل معادلته y2x جوار بما أن 2 2 lim 2 lim 2ln1 0 x x x x f x x e e فان Cfيقبل المستقيم D مقارب مائل معادلته y2x جوار 3 2 1 2 أن تحقق أ 5 x x x x x e e e e ب أدرس إشارة كل من 2 x 1 2 و e x x على e e x ln4 2 x e - - - - 0

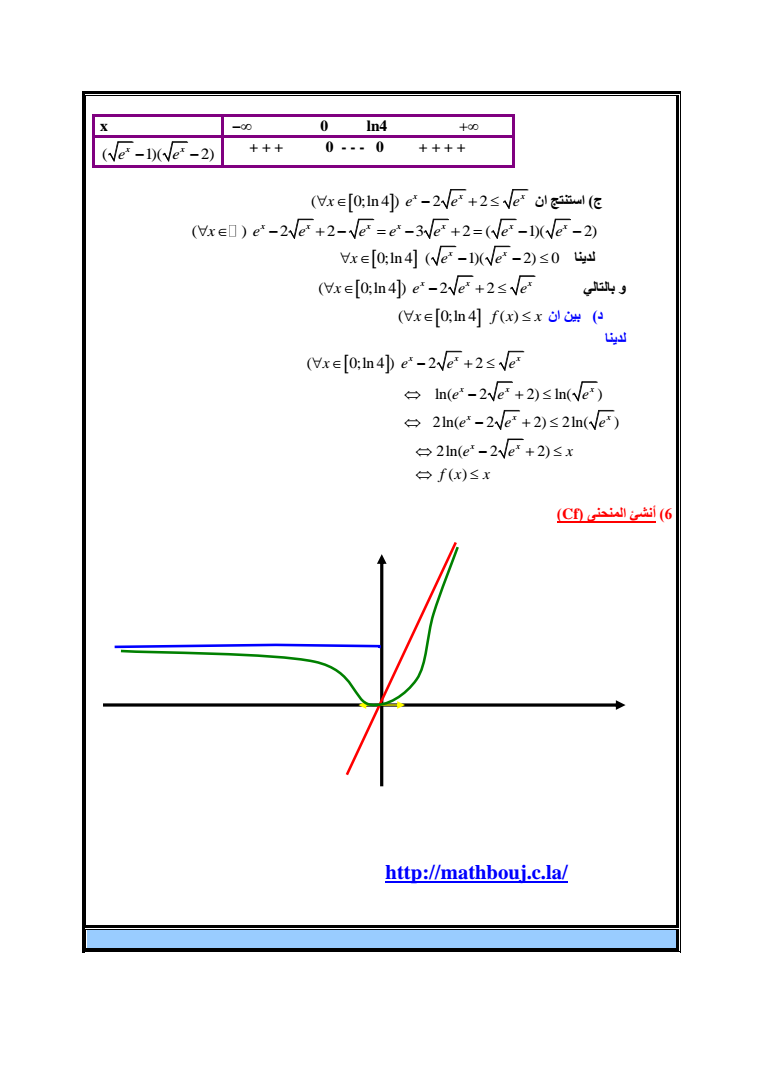
x 0 ln4 1 2 x x e e 0 - - - 0 0ln 4 2 2 ج استنتج ان x x x x e e e 2 2 3 2 1 2 x x x x x x x x e e e e e e e 0ln 4 1 2 0 لدينا x x x e e 0ln 4 2 2 بالتالي و x x x x e e e 0ln 4 x f x x د بين ان لدينا 0ln 4 2 2 ln 2 2 ln 2ln 2 2 2ln 2ln 2 2 x x x x x x x x x x x x e e e e e e e e e e e x f x x 6 أنشئ المنحنى Cf httpmathboujcla

II نعتبر المتتا لية Un المعرفة ب n من لكل U f U n n 1 و U0 1 يمكنك استعمال نتائج دراسة الدالة f n من لكل 0 ln 4 Un 1 بين بالتر جع أن من اجل n0 لدينا 0 ln 4 U0 ألن U0 1 0 ln 4 نفترض ان Un n من اجل و نبين ان 0 ln 4 Un1 0 ln 4 لدينا Un 0ln 4 و f دالة تزايدية على المجال اذن 1 0 ln 4 0 ln 4 n n f f U f U Un تناقصية 2 بين أن المتتا لية 0ln 4 x f x x لدينا 0 ln 4 بما ان Un فان n من لكل n n quot n U U n n 1 أي f U U و بالتالي المتتا لية Un تناقصية quot n U U n n 1 طريقة2 نبين بالترجع ان الن من اجل n0 لدينا U U 1 0 و U0 1 1 U ln 4 نفترض ان n اجل من U U n n 1 و نبين ان U U n n 2 1 لدينا 0ln 4 و f دالة تزايدية على المجال U U n n 1 اذن 1 n n f U f U أي U U n n 2 1 وبالتالي n U U n n 1 quot 3 Unاستنتج أن المتتا لية متقاربة ثم أحسب نهايتها Un لدينا تناقصية و مصغورة بالعدد 0 Un اذن المتتا لية متقاربة Un نحسب نهاية المتتا لية لدينا 1 U f U n n U0 0ln 4 I 0ln 4 الدالة f متصلة على المجال f 0ln4 0ln4 Un بما أن المتتا لية I 0ln 4 في المجال f x x متقاربة فان نهايتها هي حل المعادلة

0ln 4 2ln 2 2 2ln ln 2 2 ln ln 2 2 ln 2 2 x x x x x x x x x x x x x f x x f x x e e e e e e e e e e e e 3 2 0 0 4 nl او x x e e x x بما ان المتتا لية Un فان تناقصية n U U n 0 lim 0 اذن quot n U n 1 أي quot n n U